Gauss-Seidel Method

Gauss-Seidel Method

In numerical linear algebra, the Gauss–Seidel method, also known as the Liebmann method or the method of successive displacement, is an iterative method used to solve a system of a strictly diagonally dominant system of linear equations.

Procedure

1. Choose an n X n matrix

Otherwise- Show Pop up – please select the number of rows equal to the number of Columns

2. Verify that the magnitude of the diagonal item in each row of the matrix is greater than or equal to the sum of the magnitudes of all other (non-diagonal) values in that row so that

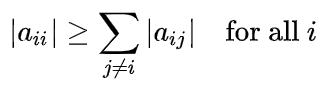
Otherwise- Show Pop up – entered matrix is not diagonally dominant

Ensure that all of the diagonal elements are non-zero as well.

a_ii ≠ 0

Otherwise- Show Pop up – all of the diagonal elements must be non-zero

3. Decompose the given matrix A into a lower triangular matrix L*, and a strictly upper triangular matrix U:

Let’s assume, A linear system of the form ��=�Ax = b

L* = $\begin{bmatrix} a11 & 0 & \cdots & 0 \\ a21 & a22 & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots \\ an1 & an2 & \cdots & ann \end{bmatrix}$;

U = $\begin{bmatrix} 0 & a12 & \cdots & a1n \\ 0 & 0 & .\ .\ . & a2n \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & 0 \end{bmatrix}$;

An upper triangular matrix differs significantly from a strictly upper triangular matrix in that an upper triangular matrix contains all zero elements below the diagonal while a strictly upper triangular matrix contains all zeroes on the diagonal also.

4. Now we’ve to choose a column matrix x⁽⁰⁾ of size n X 1 containing only 1s

x⁽⁰⁾ = $\begin{bmatrix} x1 \\ x2 \\ \vdots \\ xn \end{bmatrix}$, where, x₁ = x₂ = x₃ = . . . = x_n = 1

5. The system of linear equations can be rewritten as

Ax = b

Or, (L* + U)x = b

Or, L*x + Ux = b

Or, L*x = b – Ux

Firstly, we can only guess starting points of x, then go to the next iteration and put the updated value of x as shown in the example below

Or, x^(k+1) = L*^-1(b – Ux^(k))

Repeat the iteration process until either the value of x^(k) converges or the error, (Ax – b) becomes very tiny. For greater precision, you can choose a threshold value of 1e-8 or 1e-10. Stop the iteration procedure if the value of the error, (Ax - b), is less than 1e-8 or 1e-10. Additionally, you can initially set the program's total iterations to 1000 at the beginning.

Example

Use the iterative Gauss-Seidel method to solve the problem. There are equations

16x + 3y = 11

7x - 11y = 13

Taking values from the aforementioned equations, we obtain,

A = $\begin{bmatrix} 16 & 3 \\ 7 & - 11 \end{bmatrix}$; b = $\begin{bmatrix} 11 \\ 13 \end{bmatrix}$;

Let’s initialize, x⁽⁰⁾ =$\begin{bmatrix} 1 \\ 1 \end{bmatrix}$;

Then calculate,

1^st iteration

x⁽¹⁾ = L*^-1(b – Ux⁽⁰⁾))

= L*^-1b - L*^-1Ux⁽⁰⁾

= $\begin{bmatrix} 16 & 0 \\ 7 & - 11 \end{bmatrix}$^-1 * $\begin{bmatrix} 11 \\ 13 \end{bmatrix}$ - $\begin{bmatrix} 16 & 0 \\ 7 & - 11 \end{bmatrix}$^-1 * $\begin{bmatrix} 0 & 3 \\ 0 & 0 \end{bmatrix}$ * $\begin{bmatrix} 1 \\ 1 \end{bmatrix}$

= $\begin{bmatrix} 0.0625 & 0 \\ 0.0398 & - 0.0909 \end{bmatrix}$ * $\begin{bmatrix} 11 \\ 13 \end{bmatrix}\ $- $\begin{bmatrix} 0.0625 & 0 \\ 0.0398 & - 0.0909 \end{bmatrix}$ * $\begin{bmatrix} 0 & 3 \\ 0 & 0 \end{bmatrix}$ * $\begin{bmatrix} 1 \\ 1 \end{bmatrix}$

= $\begin{bmatrix} 0.6875 \\ - 0.7439 \end{bmatrix}$ - $\begin{bmatrix} 0 & - 0.1875 \\ 0 & - 0.1194 \end{bmatrix}$* $\begin{bmatrix} 1 \\ 1 \end{bmatrix}$

= $\begin{bmatrix} 0.5000 \\ - 0.8636 \end{bmatrix}$

2^nd Iteration

x⁽²⁾ = L*^-1(b – Ux⁽¹⁾))

= L*^-1b - L*^-1Ux⁽¹⁾

= $\begin{bmatrix} 16 & 0 \\ 7 & - 11 \end{bmatrix}$^-1 * $\begin{bmatrix} 11 \\ 13 \end{bmatrix}$ - $\begin{bmatrix} 16 & 0 \\ 7 & - 11 \end{bmatrix}$^-1 * $\begin{bmatrix} 0 & 3 \\ 0 & 0 \end{bmatrix}$ * $\begin{bmatrix} 0.5000 \\ - 0.8636 \end{bmatrix}$

= $\begin{bmatrix} 0.8494 \\ - 0.6413 \end{bmatrix}$

3^rd Iteration

x⁽³⁾ = L*^-1(b – Ux⁽²⁾))

= L*^-1b - L*^-1Ux⁽²⁾

= $\begin{bmatrix} 0.8077 \\ - 0.6678 \end{bmatrix}$

4^th Iteration

x⁽⁴⁾ = L*^-1(b – Ux⁽³⁾))

= L*^-1b - L*^-1Ux⁽³⁾

= $\begin{bmatrix} 0.8127 \\ - 0.6646 \end{bmatrix}$

5^th Iteration

x⁽⁵⁾ = L*^-1(b – Ux⁽⁴⁾))

= L*^-1b - L*^-1Ux⁽⁴⁾

= $\begin{bmatrix} 0.8121 \\ - 0.6650 \end{bmatrix}$

6^th Iteration

x⁽⁶⁾ = L*^-1(b – Ux⁽⁵⁾))

= L*^-1b - L*^-1Ux⁽⁵⁾

= $\begin{bmatrix} 0.8122 \\ - 0.6650 \end{bmatrix}$

7^th Iteration

x⁽⁷⁾ = L*^-1(b – Ux⁽⁶⁾))

= L*^-1b - L*^-1Ux⁽⁶⁾

= $\begin{bmatrix} 0.8122 \\ - 0.6650 \end{bmatrix}$

As expected, the algorithm converges to the exact solution

Now the approximate value of x and y are 0.8122 and -0.6650, respectively.

(for the programming perspective)

Repeat the iteration process until either the value of x^(k) converges or the error, (Ax – b) becomes very tiny. For greater precision, you can choose a threshold value of 1e-8 or 1e-10. Stop the iteration procedure if the value of the error, (Ax - b), is less than 1e-8 or 1e-10. Additionally, you can initially set the program's total iterations to 1000 at the beginning.