Massive MIMO Channel Model For mmWave

Massive MIMO Channel Model For mmWave

5.1. Introduction

A fundamental feature of mm wave propagation is high free-space pathloss, which introduces small amount of spatial selectivity or scattering of propagated signal paths. Large, densely packed antenna arrays, on the other hand, provide high-level antenna correlation. The widely used extended Saleh Valenzuela model (clustered channel model), that helps us to capture features accurately across Mm Wave channels.

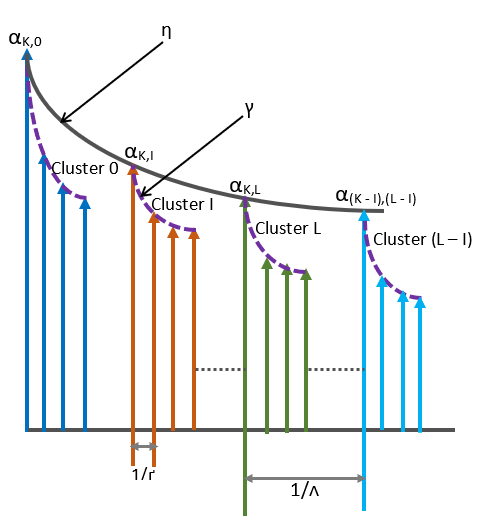
Fig 5.1: Saleh Valenzuela Channel Model distinguishing the cluster arrivals from the ray arrivals

5.2. Saleh Valenzuala Channel Model

Here in figure 5.1, it is shown Saleh Valenzuela model is basically based on amplitude and time delays of clusters and it is due to multi-paths between Tx & Rx. In figure the k^th multi-path is forming many clusters like, cluster 0, cluster 1, etc., and each cluster contains rays.

Clusters are reaching at receiver at an average decay rate and similarly, rays or MPCs in each clusters are also forming in an average decay rate. The arrival rate of clusters and MPCs within each cluster is assumed to be governed by poisson distribution process (Meijerink, 2014).

Here, symbol ‘Λ’ representing the rate of clusters in unit time and ‘Γ’ represents the ray arrival rate in unit time.

When using the clustered channel model, the channel matrix H is supposed to be the sum of the contributions in the propagated multi-paths. As a result, channel matrix H can be expressed as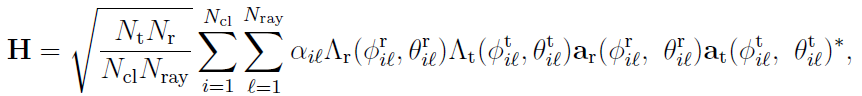

…………(5.1)

(El Ayach, 2014)

Where,Ʌ_t (ϕ^t_il θ^t_il)= Gain of antenna elements at corresponding departure angles at tx

Ʌ_r (ϕ^r_il θ^r_il)= antenna element gain at the corresponding angles of arrival at rx

a_r(ϕ^r_il θ^r_il)=normalized response vectors of antenna arrays at receiver with azimuth (elevation) angle of ϕ^r_il ( θ^r_il) and ϕ^t_il ( θ^t_il) respectively

a_r(ϕ^r_il θ^r_il)=normalized response vectors of antenna arrays at receiver with azimuth (elevation) angle of ϕ^r_il ( θ^r_il) and ϕ^t_il ( θ^t_il) respectively

5.3. Different types of antenna arrays and their array response

The array response vectors for uniform linear arrays (ULA) with elements, N are represented as

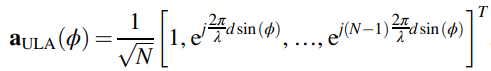……….(5.2)

Similarly, for Uniform Planer arrays (UPA), the array response vectors can be represented as,

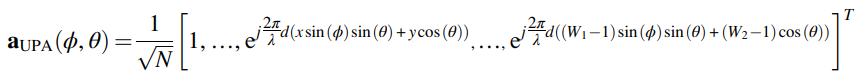
………..(5.3)

(Appendix A)

Where 0 ≤ x ≤ W₁ -1 and 0 ≤ y ≤ W₂ -1

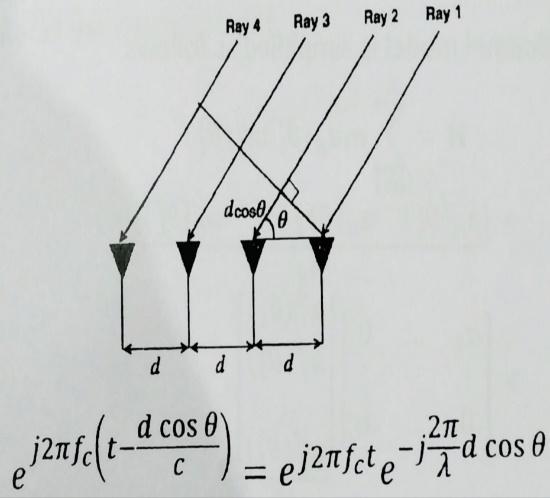
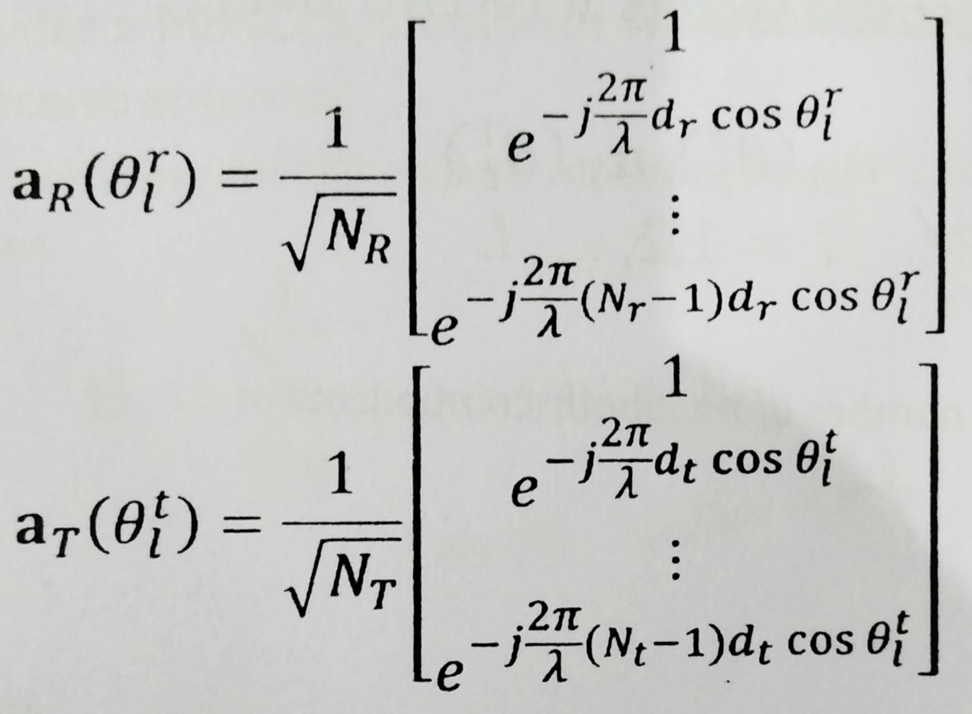
Fig 5.2: Directional cosine vectors at each antenna element (Appendix A)

In figure 5.2, it is illustrated that when transmitted signal reaches at receiver it creates different path lengths at different antenna element. Here in figure the second ray creates path-length difference of dcosθ with the first element. As there will be phase difference for same angle of departure (AOD) rays transmitted from Tx side. The corresponding calculation of phase difference is shown in figure.