Double-sideband suppressed-carrier transmission (DSB-SC) is transmission in which frequencies produced by amplitude modulation (AM) are symmetrically spaced above and below the carrier frequency and the carrier level is reduced to the lowest practical level, ideally being completely suppressed.
In the DSB-SC modulation, unlike in AM, the wave carrier is not transmitted; thus, much of the power is distributed between the sidebands, which implies an increase of the cover in DSB-SC, compared to AM, for the same power use.
DSB-SC transmission is a special case of double-sideband reduced carrier transmission. It is used for radio data systems. This model is frequently used in Amateur radio voice communications, especially on High-Frequency bands.
Spectrum
DSB-SC is basically an amplitude modulation wave without the carrier, therefore reducing power waste, and making it more efficient. This is an increase compared to normal AM transmission (DSB) that has a maximum efficiency of 33.3% since 2/3 of the power is in the carrier which conveys no useful information and both sidebands contain identical copies of the same information. Single Side Band Suppressed Carrier (SSB-SC) is 100% efficient.
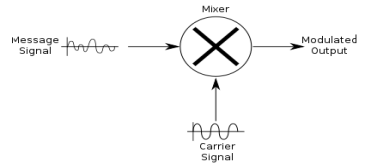
DSB-SC Modulator
DSB-SC is generated by a mixer. In its most common application, two signals are applied to a mixer, and it produces new signals at the sum and difference of the original frequencies. This consists of a message signal multiplied by a carrier signal. The mathematical representation of this process is shown below, where the product-to-sum trigonometric identity is used.
(Modulated signal)
Where, Vmcos(ωmt) is the message signal
Vccos(ωct) is the carrier signal
Normal AM modulation vs DSB-SC
Normal AM modulation process is represented as:
where m is the modulation index. In case of AM Modulation carrier is modulated by varying amplitude linearly proportional to baseband signal.
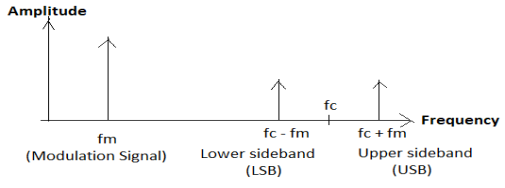
Theoretically, the amplitude-modulated wave has three frequencies. Those are carrier frequency fc, upper sideband frequency fc + fm, and lower sideband frequency fc - fm. After modulation, this signal in the frequency domain looks like this:
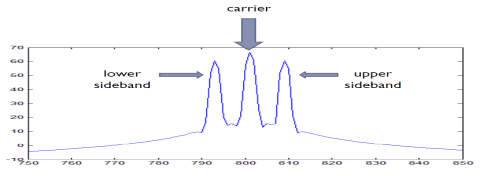
We know the information is in sidebands. So there is no need to send only carrier frequency when it consumes 50% of the total transmitted power. This system will be more efficient when we send only a single sideband as sidebands containing identical copies of the same information and construct another sideband from the transmitted one. We basically follow this procedure in a single sideband suppressed carrier (SSB-SC) modulation process.
Efficiency of DSB-SC modulation
Where sidebands contain power 0.25m2Ac2 (say, Psb) and carrier frequency contains power 0.5Ac2 (say Pc). In the case of DSB-SC we transmit sidebands and suppress the carrier. So, efficiency of a DSB-SC signal is calculated as:
= [0.25m2Ac2 / (0.5Ac2 + 0.25m2Ac2)] < (1/3)
For AM, less than 33% of the power is in the sidebands. For DSB, 100% of the power is the sidebands.
DSB-SC Detector
For DSBSC, Coherent Demodulation is done by multiplying the DSB-SC signal with the carrier signal (with the same phase as in the modulation process) just like the modulation process. This resultant signal is then passed through a low pass filter to produce a scaled version of the original message signal.
= (1/2. Vc. Vc‘)Vm cos(ωmt) + (1/4. Vc. Vc‘Vm) [cos((ωm + 2ωc)t) + cos((ωm - 2ωc)t)]
The equation above shows that by multiplying the modulated signal by the carrier signal, the result is a scaled version of the original message signal plus a second term. Since ωc >> ωm, this second term is much higher in frequency than the original message signal. Once the signal passes through a lowpass filter, the higher frequency component is removed, leaving the original message signal.
Q & A and Summary
Q1: What does DSB-SC stand for, and how does it differ from conventional AM?
DSB-SC stands for Double Sideband Suppressed Carrier. Unlike conventional Amplitude Modulation (AM), which transmits the carrier along with the sidebands, DSB-SC suppresses the carrier, transmitting only the sidebands. This results in more power efficiency and bandwidth utilization.
Q2: What is the mathematical expression for a DSB-SC modulated signal?
The DSB-SC signal \( s(t) \) is given by: \( s(t) = A_c m(t) \cos(2\pi f_c t) \)
where \( A_c \) is the carrier amplitude, \( m(t) \) is the message signal, and \( f_c \) is the carrier frequency.
Q3: Why is the carrier not transmitted in DSB-SC?
The carrier does not contain useful information. Transmitting it would waste power. By suppressing the carrier, DSB-SC systems become more energy-efficient.
Q4: Explain the frequency domain representation of DSB-SC.
The frequency-domain representation is: \( S(j\omega) = \frac{1}{2} \left[ M(j(\omega - \omega_c)) + M(j(\omega + \omega_c)) \right] \)
This shows that the message spectrum is shifted to both \( +\omega_c \) and \( -\omega_c \), creating upper and lower sidebands.
Q5: What is the role of a coherent detector in DSB-SC demodulation?
A coherent detector multiplies the received signal with a locally generated carrier that is in phase and frequency sync with the original. Any phase or frequency mismatch results in distortion of the demodulated signal.
Q6: What distortion occurs if synchronization is not perfect during demodulation?
Imperfect synchronization leads to phase or frequency mismatch. This results in signal distortion and loss of message fidelity during recovery.
Q7: Why is a Low Pass Filter (LPF) used after coherent detection?
After coherent detection, the product contains both baseband and high-frequency components (at double the carrier frequency). The LPF removes high-frequency components, isolating the original baseband message.
Q8: What happens in the frequency spectrum when a message signal is modulated using DSB-SC?
The spectrum of the message signal \( M(j\omega) \) is shifted to center around \( +\omega_c \) and \( -\omega_c \). This produces two symmetrical sidebands (USB and LSB) and the carrier is not present.
Q9: Can DSB-SC be demodulated without using the exact same carrier frequency?
No, DSB-SC requires exact carrier frequency and phase for coherent demodulation. Any deviation leads to inaccurate recovery of the message signal.
Q10: What are the key advantages and disadvantages of DSB-SC?
Advantages: Efficient use of power, better bandwidth usage.
Disadvantages: Requires complex coherent detection and exact carrier synchronization.