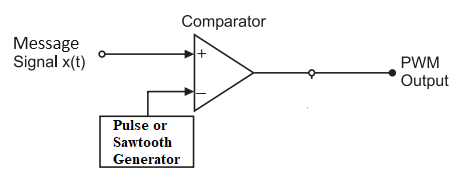
MATLAB Code for Pulse Width Modulation (PWM) and Demodulation

MATLAB Code for Analog Pulse Width Modulation (PWM)

clc;
clear all;
close all;
fs=30; %frequency of the sawtooth signal
fm=3; %frequency of the message signal
sampling_frequency = 10e3;
a=0.5; % amplitide

t=0:(1/sampling_frequency):1; %sampling rate of 10kHz

sawtooth=2*a.*sawtooth(2*pi*fs*t); %generating a sawtooth wave

subplot(4,1,1);
plot(t,sawtooth); % plotting the sawtooth wave
title('Comparator Wave');

msg=a.*sin(2*pi*fm*t); %generating message wave

subplot(4,1,2);
plot(t,msg); %plotting the sine message wave
title('Message Signal');

for i=1:length(sawtooth)
if (msg(i)>=sawtooth(i))
pwm(i)=1; %is message signal amplitude at i th sample is greater than
%sawtooth wave amplitude at i th sample
else
pwm(i)=0;
end
end

subplot(4,1,3);
plot(t,pwm,'r');
title('PWM');
axis([0 1 0 1.1]); %to keep the pwm visible during plotting.

%% Demodulation
% Demodulation: Measure the pulse width to reconstruct the signal
demodulated_signal = zeros(size(msg));

for i = 1:length(pwm)-1
if pwm(i) == 1
% Measure the time until the next falling edge
j = i + 1;
while pwm(j) == 1 && j < length(pwm)
j = j + 1;
end
% Reconstruct the analog value based on pulse width
demodulated_signal(i) = mean(msg(i:j-1));
end
end

% Low-Pass Filter Design
Fs = 1 / (t(2) - t(1)); % Sampling frequency
Fc = 5; % Cutoff frequency (adjust based on your signal)
[b, a] = butter(4, Fc / (Fs / 2), 'low'); % 4th-order Butterworth filter

% Apply the Low-Pass Filter
filtered_signal = filtfilt(b, a, demodulated_signal);

% Plot the demodulated and filtered signal for comparison
subplot(4,1,4);
plot(t, filtered_signal, 'r', 'LineWidth', 1.5); % Filtered signal in red
title('Demodulated Signal (Filtered)');
xlabel('Time');
ylabel('Amplitude');
grid on;

Output

MATLAB Code for Digital Pulse Width Modulation (PWM)


% This code is developed by SalimWireless.Com
clc; clear; close all;
% Digital SPWM Generator using Square Wave Carrier in MATLAB

% === PARAMETERS ===
fs_carrier = 20;       % Carrier frequency in Hz
f_signal = 5;           % Message signal frequency in Hz
sampleRate = 50000;      % Samples per second
duration = 1;            % Duration in seconds

% === TIME VECTOR ===
t = linspace(0, duration, sampleRate * duration);

% === MESSAGE SIGNAL (SINE WAVE) ===
signal = sin(2 * pi * f_signal * t);

% === NORMALIZE SIGNAL TO 0–1 FOR DUTY CYCLE ===
normalizedSignal = (signal + 1) / 2;  % Scale from [-1, 1] to [0, 1]

% === PWM GENERATION BASED ON SQUARE CARRIER PERIODS ===
samplesPerCarrierPeriod = floor(sampleRate / fs_carrier);
pwm = zeros(1, length(t));

% Generate PWM: For each carrier cycle, set ON time based on message amplitude at start
for i = 1:samplesPerCarrierPeriod:length(t)
    startIndex = i;
    if startIndex > length(t)
        break;
    end
    
    % Duty cycle at start of period
    duty = normalizedSignal(startIndex);
    onSamples = floor(samplesPerCarrierPeriod * duty);
    
    % Set PWM high for onSamples
    endIndex = min(startIndex + samplesPerCarrierPeriod - 1, length(t));
    onEndIndex = min(startIndex + onSamples - 1, endIndex);
    
    pwm(startIndex:onEndIndex) = 1;
end

% === GENERATE SQUARE CARRIER FOR REFERENCE PLOTTING ===
carrierSquare = double(mod(t * fs_carrier, 1) < 0.5);

% === TRIM TO FIRST 3 CYCLES OF MESSAGE SIGNAL FOR VISUALIZATION ===
samplesToPlot = floor(3 * (sampleRate / f_signal));
t_plot = t(1:samplesToPlot);
signal_plot = signal(1:samplesToPlot);
carrier_plot = carrierSquare(1:samplesToPlot);
pwm_plot = pwm(1:samplesToPlot);

% === PLOTTING ===
figure('Name', 'PWM with Square Wave Carrier', 'Color', 'w');
hold on;
plot(t_plot, signal_plot, 'b', 'LineWidth', 1.2);
plot(t_plot, carrier_plot, 'g--', 'LineWidth', 1);
stairs(t_plot, pwm_plot, 'r', 'LineWidth', 1.2);
hold off;

xlabel('Time (s)');
ylabel('Amplitude');
title('PWM Output with Square Wave Carrier');
legend('Message Signal (Sine)', 'Square Carrier', 'PWM Output', 'Location', 'southoutside', 'Orientation', 'horizontal');
grid on;
web('https://www.salimwireless.com/search?q=pwm%20pulse%20modulation', '-browser');

Output

Parameter	PAM	PWM	PPM	DM	PCM
Parameter varied	Signal amplitude	Pulse duration	Pulse timing	Sample difference (delta)	Digital code
Pulse duration	Fixed	Adjustable	Fixed	Fixed	Fixed
Resistance to noise	Poor	Average	Good	Average	Good
Bandwidth requirement	Low	Moderate	High	Low	High
Implementation complexity	Low	Medium	High	Low	High
MATLAB implementation	PAM Script	PWM Script	PPM Script	DM Script	PCM Script
Further reading	PAM	PWM	PPM	DM	PCM

PWM Signal Generation

Click here to see how a PWM signal is generated

Search This Blog