Skip to main content

MATLAB Code for Pulse Width Modulation (PWM) and Demodulation


 

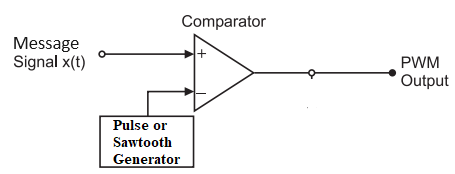
MATLAB Code for Analog Pulse Width Modulation (PWM)

clc;
clear all;
close all;
fs=30; %frequency of the sawtooth signal
fm=3; %frequency of the message signal
sampling_frequency = 10e3;
a=0.5; % amplitide

t=0:(1/sampling_frequency):1; %sampling rate of 10kHz


sawtooth=2*a.*sawtooth(2*pi*fs*t); %generating a sawtooth wave


subplot(4,1,1);
plot(t,sawtooth); % plotting the sawtooth wave
title('Comparator Wave');

msg=a.*sin(2*pi*fm*t); %generating message wave

subplot(4,1,2);
plot(t,msg); %plotting the sine message wave
title('Message Signal');


for i=1:length(sawtooth)
if (msg(i)>=sawtooth(i))
pwm(i)=1; %is message signal amplitude at i th sample is greater than
%sawtooth wave amplitude at i th sample
else
pwm(i)=0;
end
end

subplot(4,1,3);
plot(t,pwm,'r');
title('PWM');
axis([0 1 0 1.1]); %to keep the pwm visible during plotting.

%% Demodulation
% Demodulation: Measure the pulse width to reconstruct the signal
demodulated_signal = zeros(size(msg));

for i = 1:length(pwm)-1
if pwm(i) == 1
% Measure the time until the next falling edge
j = i + 1;
while pwm(j) == 1 && j < length(pwm)
j = j + 1;
end
% Reconstruct the analog value based on pulse width
demodulated_signal(i) = mean(msg(i:j-1));
end
end

% Low-Pass Filter Design
Fs = 1 / (t(2) - t(1)); % Sampling frequency
Fc = 5; % Cutoff frequency (adjust based on your signal)
[b, a] = butter(4, Fc / (Fs / 2), 'low'); % 4th-order Butterworth filter

% Apply the Low-Pass Filter
filtered_signal = filtfilt(b, a, demodulated_signal);

% Plot the demodulated and filtered signal for comparison
subplot(4,1,4);
plot(t, filtered_signal, 'r', 'LineWidth', 1.5); % Filtered signal in red
title('Demodulated Signal (Filtered)');
xlabel('Time');
ylabel('Amplitude');
grid on;
 

Output 



 MATLAB Code for Digital Pulse Width Modulation (PWM)


% This code is developed by SalimWireless.Com
clc; clear; close all;
% Digital SPWM Generator using Square Wave Carrier in MATLAB

% === PARAMETERS ===
fs_carrier = 20;       % Carrier frequency in Hz
f_signal = 5;           % Message signal frequency in Hz
sampleRate = 50000;      % Samples per second
duration = 1;            % Duration in seconds

% === TIME VECTOR ===
t = linspace(0, duration, sampleRate * duration);

% === MESSAGE SIGNAL (SINE WAVE) ===
signal = sin(2 * pi * f_signal * t);

% === NORMALIZE SIGNAL TO 0–1 FOR DUTY CYCLE ===
normalizedSignal = (signal + 1) / 2;  % Scale from [-1, 1] to [0, 1]

% === PWM GENERATION BASED ON SQUARE CARRIER PERIODS ===
samplesPerCarrierPeriod = floor(sampleRate / fs_carrier);
pwm = zeros(1, length(t));

% Generate PWM: For each carrier cycle, set ON time based on message amplitude at start
for i = 1:samplesPerCarrierPeriod:length(t)
    startIndex = i;
    if startIndex > length(t)
        break;
    end
    
    % Duty cycle at start of period
    duty = normalizedSignal(startIndex);
    onSamples = floor(samplesPerCarrierPeriod * duty);
    
    % Set PWM high for onSamples
    endIndex = min(startIndex + samplesPerCarrierPeriod - 1, length(t));
    onEndIndex = min(startIndex + onSamples - 1, endIndex);
    
    pwm(startIndex:onEndIndex) = 1;
end

% === GENERATE SQUARE CARRIER FOR REFERENCE PLOTTING ===
carrierSquare = double(mod(t * fs_carrier, 1) < 0.5);

% === TRIM TO FIRST 3 CYCLES OF MESSAGE SIGNAL FOR VISUALIZATION ===
samplesToPlot = floor(3 * (sampleRate / f_signal));
t_plot = t(1:samplesToPlot);
signal_plot = signal(1:samplesToPlot);
carrier_plot = carrierSquare(1:samplesToPlot);
pwm_plot = pwm(1:samplesToPlot);

% === PLOTTING ===
figure('Name', 'PWM with Square Wave Carrier', 'Color', 'w');
hold on;
plot(t_plot, signal_plot, 'b', 'LineWidth', 1.2);
plot(t_plot, carrier_plot, 'g--', 'LineWidth', 1);
stairs(t_plot, pwm_plot, 'r', 'LineWidth', 1.2);
hold off;

xlabel('Time (s)');
ylabel('Amplitude');
title('PWM Output with Square Wave Carrier');
legend('Message Signal (Sine)', 'Square Carrier', 'PWM Output', 'Location', 'southoutside', 'Orientation', 'horizontal');
grid on;
web('https://www.salimwireless.com/search?q=pwm%20pulse%20modulation', '-browser');

Output

 
Parameter PAM PWM PPM DM PCM
Parameter varied Signal amplitude Pulse duration Pulse timing Sample difference (delta) Digital code
Pulse duration Fixed Adjustable Fixed Fixed Fixed
Resistance to noise Poor Average Good Average Good
Bandwidth requirement Low Moderate High Low High
Implementation complexity Low Medium High Low High
MATLAB implementation PAM Script PWM Script PPM Script DM Script PCM Script
Further reading PAM PWM PPM DM PCM

PWM Signal Generation

 

 
 
 

Further Reading

People are good at skipping over material they already know!

View Related Topics to







Contact Us

Name

Email *

Message *

Popular Posts

BER vs SNR for M-ary QAM, M-ary PSK, QPSK, BPSK, ...(MATLAB Code + Simulator)

Bit Error Rate (BER) & SNR Guide Analyze communication system performance with our interactive simulators and MATLAB tools. 📘 Theory 🧮 Simulators 💻 MATLAB Code 📚 Resources BER Definition SNR Formula BER Calculator MATLAB Comparison 📂 Explore M-ary QAM, PSK, and QPSK Topics ▼ 🧮 Constellation Simulator: M-ary QAM 🧮 Constellation Simulator: M-ary PSK 🧮 BER calculation for ASK, FSK, and PSK 🧮 Approaches to BER vs SNR What is Bit Error Rate (BER)? The BER indicates how many corrupted bits are received compared to the total number of bits sent. It is the primary figure of merit for a...
Read more

Constellation Diagrams of ASK, PSK, and FSK (with MATLAB Code + Simulator)

Constellation Diagrams: ASK, FSK, and PSK Comprehensive guide to signal space representation, including interactive simulators and MATLAB implementations. 📘 Overview 🧮 Simulator ⚖️ Theory 📚 Resources Definitions Constellation Tool Key Points MATLAB Code 📂 Other Topics: M-ary PSK & QAM Diagrams ▼ 🧮 Simulator for M-ary PSK Constellation 🧮 Simulator for M-ary QAM Constellation BASK (Binary ASK) Modulation Transmits one of two signals: 0 or -√Eb, where Eb​ is the energy per bit. These signals represent binary 0 and 1. BFSK (Binary FSK) Modulation Transmits one ...
Read more

DFTs-OFDM vs OFDM: Why DFT-Spread OFDM Reduces PAPR Effectively (with MATLAB Code)

DFT-spread OFDM (DFTs-OFDM) has lower Peak-to-Average Power Ratio (PAPR) because it "spreads" the data in the frequency domain before applying IFFT, making the time-domain signal behave more like a single-carrier signal rather than a multi-carrier one like OFDM. Deeper Explanation: Aspect OFDM DFTs-OFDM Signal Type Multi-carrier Single-carrier-like Process IFFT of QAM directly QAM → DFT → IFFT PAPR Level High (due to many carriers adding up constructively) Low (less fluctuation in amplitude) Why PAPR is High Subcarriers can add in phase, causing spikes DFT "pre-spreads" data, smoothing it Used in Wi-Fi, LTE downlink LTE uplink (as SC-FDMA) In OFDM, all subcarriers can...
Read more

Online Simulator for ASK, FSK, and PSK

Try our new Digital Signal Processing Simulator!   •   Interactive ASK, FSK, and BPSK tools updated for 2025. Start Now Interactive Modulation Simulators Visualize binary modulation techniques (ASK, FSK, BPSK) in real-time with adjustable carrier and sampling parameters. 📡 ASK Simulator 📶 FSK Simulator 🎚️ BPSK Simulator 📚 More Topics ASK Modulator FSK Modulator BPSK Modulator More Topics Simulator for Binary ASK Modulation Digital Message Bits Carrier Freq (Hz) Sampling Rate (...
Read more

Power Distribution in Amplitude Modulation (AM)

Power Distribution In practice, the AM wave s(t) is a voltage or current signal. In either case, the average power delivered to a 1-ohm load resistor by s(t) is comprised of three components: Carrier power = (1/2) A c 2 Upper side-frequency power = (1/8)μ 2 A c 2 Lower side-frequency power = (1/8)μ 2 A c 2 The ratio of the total sideband power to the total power in the modulated wave is therefore equal to μ 2 / (2 + μ 2 ), which depends only on the modulation factor μ. If μ = 1, that is, 100% modulation is used, the total power in the two side-frequencies of the resulting AM wave is only one-third of the total power in the modulated wave. A major topic in Amplitude Modula...
Read more

Filter Bank Multicarrier (FBMC)

Filter Bank Multicarrier (FBMC) Filter Bank Multicarrier (FBMC) is an advanced multicarrier modulation technique designed to overcome the spectral inefficiencies and interference issues of OFDM. Motivation: Limitations of OFDM In an OFDM system , the transmitter uses an Inverse Fast Fourier Transform (IFFT) and the receiver uses a Fast Fourier Transform (FFT) to process multiple subcarriers. Each OFDM symbol occupies a duration denoted by T sym . OFDM is a multicarrier modulation technique where a high data-rate stream is divided into multiple parallel low data-rate streams. To mitigate inter-symbol interference (ISI) caused by multipath fading, the total bandwidth B is divided into N narrow sub-bands. However, a major drawback of OFDM is that the subcarrier filters generated by the IFFT/FFT process have poor spectral cont...
Read more

OFDM vs SC-OFDM

  The main difference between OFDM and SC-OFDM is that SC-OFDM transmits the signal using a single carrier, while OFDM uses multiple subcarriers. However, in SC-OFDM, the signal is generated with different sub-bands, but it is transmitted through a single carrier (more technically, through a wideband carrier signal). Block Diagram of OFDM: Data → Modulation → Serial-to-Parallel → IFFT → Add CP → Transmit Received Signal → Remove CP → FFT → Parallel-to-Serial → Demodulation → Data Block Diagram of SC-OFDM: Data → Modulation → DFT → IFFT → Add CP → Transmit Received Signal → Remove CP → FFT → Demodulation → Data    In the case of OFDM, the input modulated data is converted from a serial stream to parallel streams, and different subcarriers are assigned to each chunk. Then, IFFT is applied to these chunks, and a cyclic prefix is added to each one. Each chunk is technically referred to as an OFDM symbol . Unlike OFDM, SC-OFDM does not perform serial-to-parallel conversion o...
Read more